| 笑わない数学 第2シリーズ 結び目理論 NHK総合 2023年10月25日23:00放送 |
[NO.1600] 『数学者たちの黒板』(ジェシカ・ワイン著、徳田功 訳、草思社 刊、2023年) のなかに セハール・カーン(SAHAR KHAN) が書いたものを見つけたときから、ずっと気になっていました。 この黒板には、結び目と呼ばれる数学的対象がいくつか描かれてい たからです。
タイミングよく、今回のテーマが 結び目理論。待ってました!!
「結び目理論」とは「ひも」にできた結び目を分類する数学の一分野。様々な結び目をひもを切らずに変形していく場合、どうやっても一致させられない結び目は何種類あるのか? 数学者が頭の中で考え出した遊びのような研究は20世紀に大発展を遂げる。ところがその理論が宇宙法則と関係していたという意外な事実が! 数学は数学者の「発明」か?それとも人類とは無関係に宇宙に存在し、それを数学者が「発見」しただけなのか?
今回、いちばん気になったのが行列式でした。
◆ ◆
そもそもなぜ、二つの結び目が同じなのか、違うのかを見極めることが難しいのか。
それは、結び目の形が自在に変化してしまうことにあります。
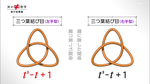
たとえば、この「三つ葉結び目(右手型)」。ほんの少し形を変えるだけで、ほら最初と同じなのかどうか、怪しくなってきます。結び目は、やろうと思えば、いくらでも複雑な形に変えることが出来るのです。見た目だけで、同じかどうかを判断することは至難の業なのです。
でも、もし変化したとしても、同じかどうかを見極める「何か」があったとしたらどうか? たとえば、いくら変装したとしても変わらない「指紋」のようなものが結び目にもあればいい。
結び目の指紋(不変量)を探すことが、数学者たちの目標となりました。結び目が同じなのか違うのか、数学的にきっちり判定する方法を見つけ出そうというのです。
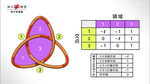
1928年 ジェームズ・アレクサンダー(1888-1971)が、アレクサンダー多項式を発見。
結び目を形づくる、ひもの交点やひもが囲む領域の位置をたよりに、結び目を数式に置き換えたものです。
たとえ結び目が形を変えて変装したとしても、その数式は変わりません。まさに変装しても変わらない指紋のような特徴があるのです。
このアレクサンダーの大発見は、それまで手探りだった結び目へのアプローチをちゃんとした数学の一分野へと押し上げたのです。
でも、アレクサンダー多項式には弱点がありました。「三つ葉結び目(右手型)」と「三つ葉結び目(左手型)」は違うのに、同じ数式になってしまいました。鏡で映した関係の結び目を区別できないという弱点があったのです。
1984年 ヴォーン・ジョーンズ(1952-2020)
ジョーンズ多項式
その数ヶ月後
HOMFLYPT多項式
1993年 コンツェビッチ不変量
◆ ◆
エドワード・ウィッテン博士(プリンストン高等研究所 教授)
「量子場の理論とジョーンズ多項式」(1989年)
じつは、数学者たちが(遊びで)勝手に作り出したはずの「結び目理論」が、人間とは関係なく存在するはずの自然法則の中に、宇宙誕生当初から組み込まれていた可能性を示しているというのです。
マリオ・リヴィオ博士(ネバダ大学ラスベガス校 宇宙物理学者)
数学史に詳しいマリオ・リヴィオ博士。
人間が作り出したた数学が、なぜか宇宙とつながっているという事実は、根源的な謎を私たちに問いかけていると語ります。
これはとても驚くべきことです。数学が持つ信じられないほどの力を示しているのです。数学者はもともと何かに役立つことを目指して数学を研究しているわけではないのに、実際には物理現象の解明に数学が大いに役立つのですから。
結び目理論と宇宙法則との驚くべきつながりは、数学は人間が自ら頭の中で作り出した発明なのか?
それとも人間とは関係なく大昔から存在していたものを、人間がたまたま発見したものなのか? という深遠なる問いを投げかけているのです。
◆ ◆
数学は数学者が頭の中で勝手に作り出した発明なのか。それともこの宇宙に人類が存在する前からあって、それを人類が後から発見しただけなのか、というこの哲学的な疑問。
結び目理論そ追ってきて、思いもよらぬことにたどり着いてしまいました。
思い返してみると、あの非ユークリッド幾何学だって、人間が勝手に空想したものに過ぎないって、思っていたら、じつはこの世界が非ユークリッド幾何学でできていた、ってことがありましたよね。
人類による発明だと思っていた数学が、じつはいわば神様がそれを大昔から使っていて、人間はそれにようやく気づいただけなのかもしれない。
















コメント